平衡二叉树和AVL树

平衡二叉树

平衡二叉树：对于任意一个节点，左子树和右子树的高度差不能超过1

平衡二叉树的高度和节点数量之间的关系也是 O(log N)

什么是平衡二叉树

二分搜索树可以表示动态的数据集合，对于给定的数据集合，在建立一颗二分搜索树时，二分搜索树的结构形态与关键字的插入顺序有关。如果全部或者部分地按照关键字的递增或者递减顺序插入二分搜索树的结点，则所建立的二分搜索树全部或者在局部形成退化的单分支结构。

在最坏的情况下，二分搜索树可能完全偏斜，高度为n，其平均与最坏的情况下查找时间都是O(n)；而最好的情况下，二分搜索树的结点尽可能靠近根结点，其平均与最好情况的查找时间都是O(logn)。因此，我们希望最理想的状态下是使二分搜索树始终处于良好的结构形态。

实现平衡二叉树

我们可以使用之前文章实现的 “二分搜索树的实现” 作为底层代码进行修改

(点击这里查看文章) 实现二分搜索树

点击下载-AVLTree.java

public class AVLTree<K extends Comparable<K>, V> {

    private class Node{
        public K key;
        public V value;
        public Node left, right;
        public int height;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            height = 1;
        }
    }

    private Node root;
    private int size;

    public AVLTree(){
        root = null;
        size = 0;
    }
}

计算节点高度及平衡因子

节点高度：节点的高度。

平衡因子：左子树的高度 减去 右子树的高度 即为该节点的平衡因子。（平衡二叉树的平衡因子只能为1，0，-1）

// 获得节点node的高度
private int getHeight(Node node){
    if(node == null)
        return 0;
    return node.height;
}

// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
    if(node == null)
        return 0;
    return getHeight(node.left) - getHeight(node.right);
}

检查二分搜索树性质及平衡性

检查BST：将该树下的所有节点通过中序遍历存储于数组中，如果升序排列，即是二分搜索树

// 判断该二叉树是否是一棵二分搜索树
public boolean isBST(){

    ArrayList<K> keys = new ArrayList<>();
    inOrder(root, keys);
    for(int i = 1 ; i < keys.size() ; i ++)
        if(keys.get(i - 1).compareTo(keys.get(i)) > 0)
            return false;
    return true;
}

private void inOrder(Node node, ArrayList<K> keys){

    if(node == null)
        return;

    inOrder(node.left, keys);
    keys.add(node.key);
    inOrder(node.right, keys);
}

检查平衡性：如果树中每一个节点的平衡因子均为 1，0，-1中的数，即是平衡二叉树

// 判断该二叉树是否是一棵平衡二叉树
public boolean isBalanced(){
    return isBalanced(root);
}

// 判断以Node为根的二叉树是否是一棵平衡二叉树，递归算法
private boolean isBalanced(Node node){

    if(node == null)
        return true;

    int balanceFactor = getBalanceFactor(node);
    if(Math.abs(balanceFactor) > 1)
        return false;
    return isBalanced(node.left) && isBalanced(node.right);
}

旋转基本原理

在平衡二叉树中删除或插入节点后，可能会使某些节点的平衡因子的绝对值大于 ，即树失去了平衡，这时候就需要进行平衡调整，使其重新满足平衡二叉树的要求。

调整平衡二叉树之前，首先要明白一个定义：最小不平衡子树。最小不平衡子树是指以离插入节点最近、且平衡因子绝对值大于1的节点做根的子树。

左旋转和右旋转

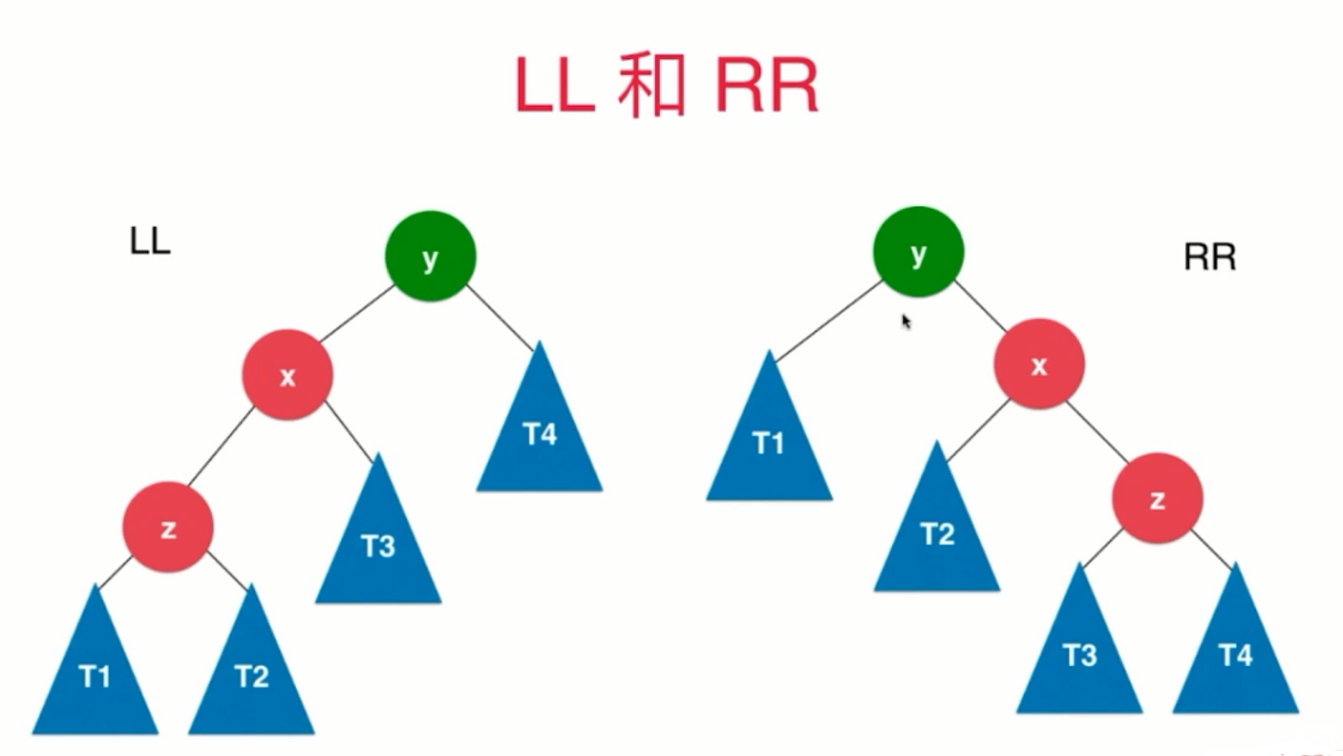
LL：新插入的节点 在 最小不平衡子树的根节点 的左侧的左侧，需要进行右旋转。

RR：新插入的节点 在 最小不平衡子树的根节点 的右侧的右侧，需要进行左旋转。

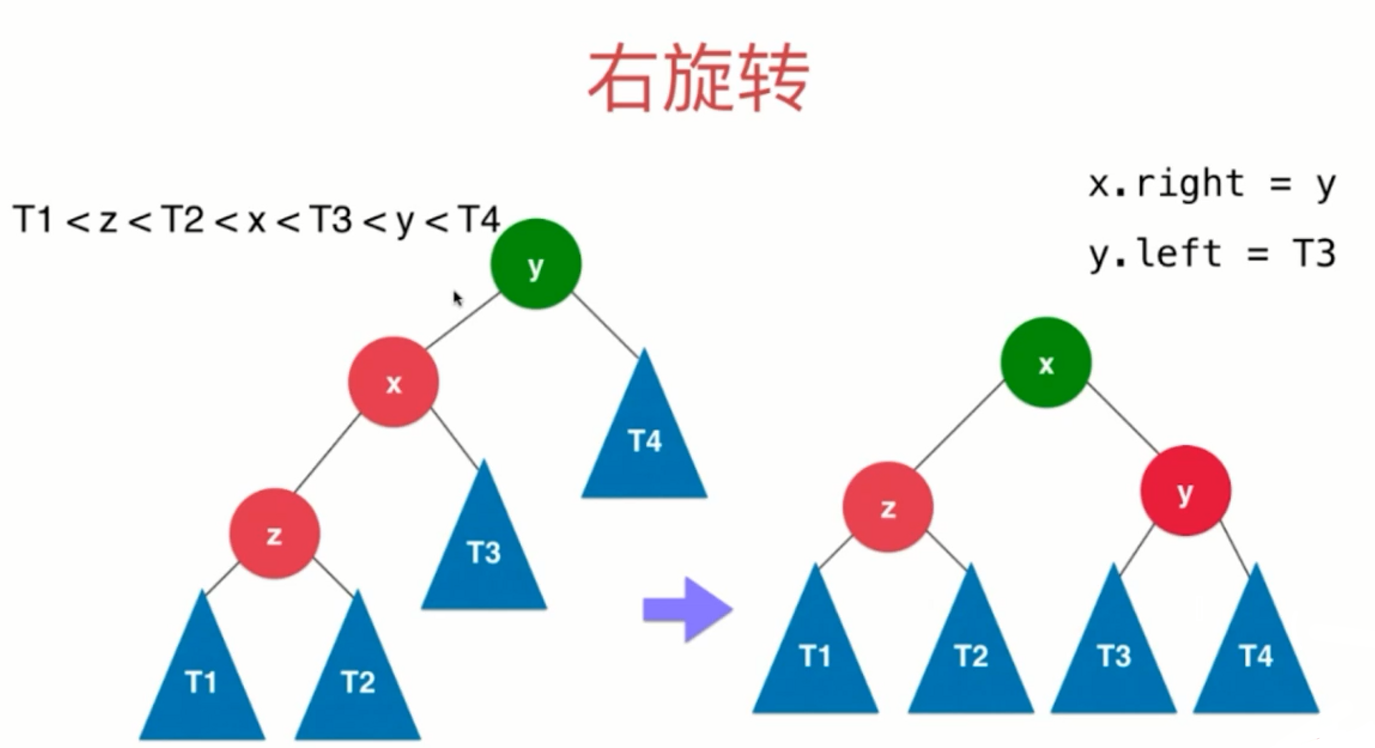
// 对节点y进行向右旋转操作，返回旋转后新的根节点x
//        y                              x
//       / \                           /   \
//      x   T4     向右旋转 (y)        z     y
//     / \       - - - - - - - ->    / \   / \
//    z   T3                       T1  T2 T3 T4
//   / \
// T1   T2
private Node rightRotate(Node y) {
    Node x = y.left;
    Node T3 = x.right;

    // 向右旋转过程
    x.right = y;
    y.left = T3;

    // 更新height
    y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
    x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

    return x;
}

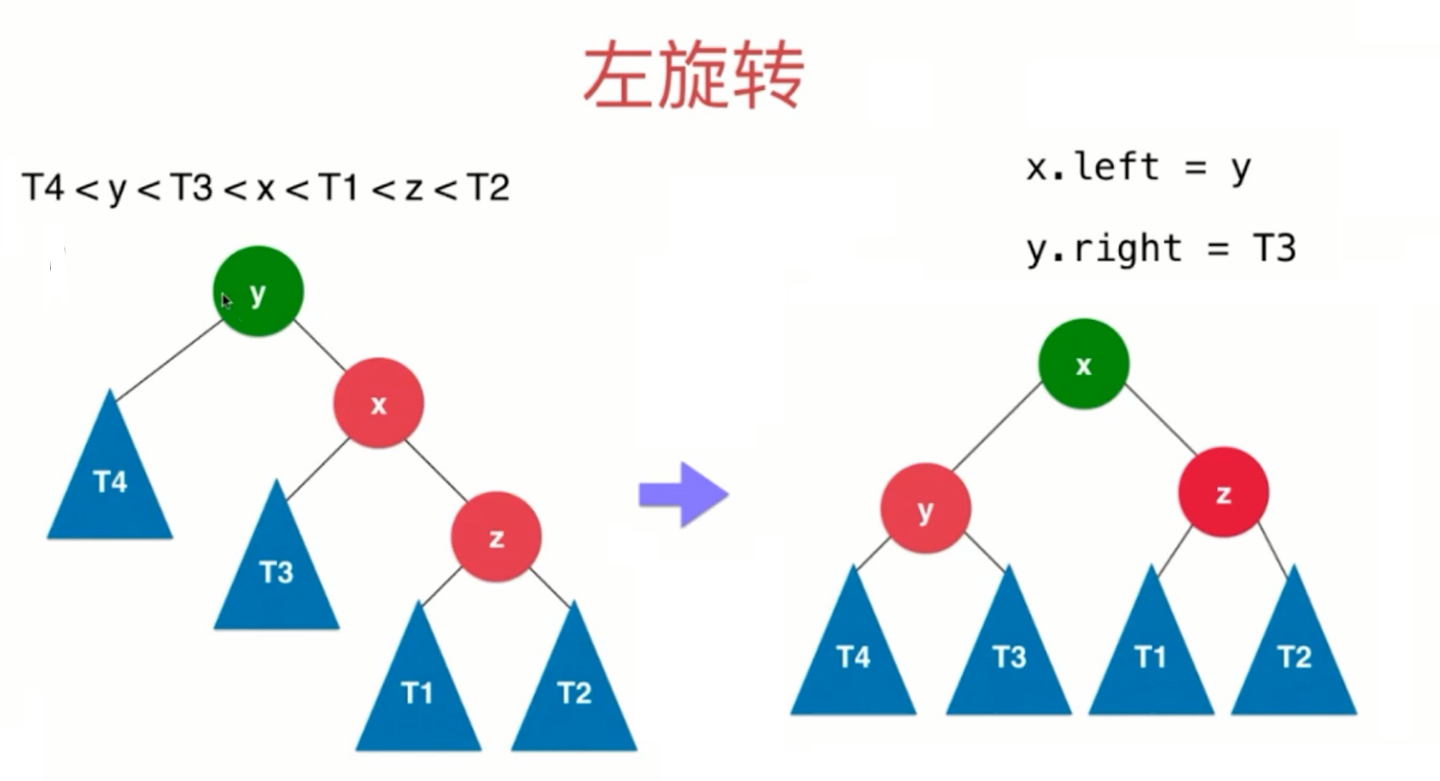
// 对节点y进行向左旋转操作，返回旋转后新的根节点x
//    y                             x
//  /  \                          /   \
// T1   x      向左旋转 (y)       y     z
//     / \   - - - - - - - ->   / \   / \
//   T2  z                     T1 T2 T3 T4
//      / \
//     T3 T4
private Node leftRotate(Node y) {
    Node x = y.right;
    Node T2 = x.left;

    // 向左旋转过程
    x.left = y;
    y.right = T2;

    // 更新height
    y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
    x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

    return x;
}

LR和RL

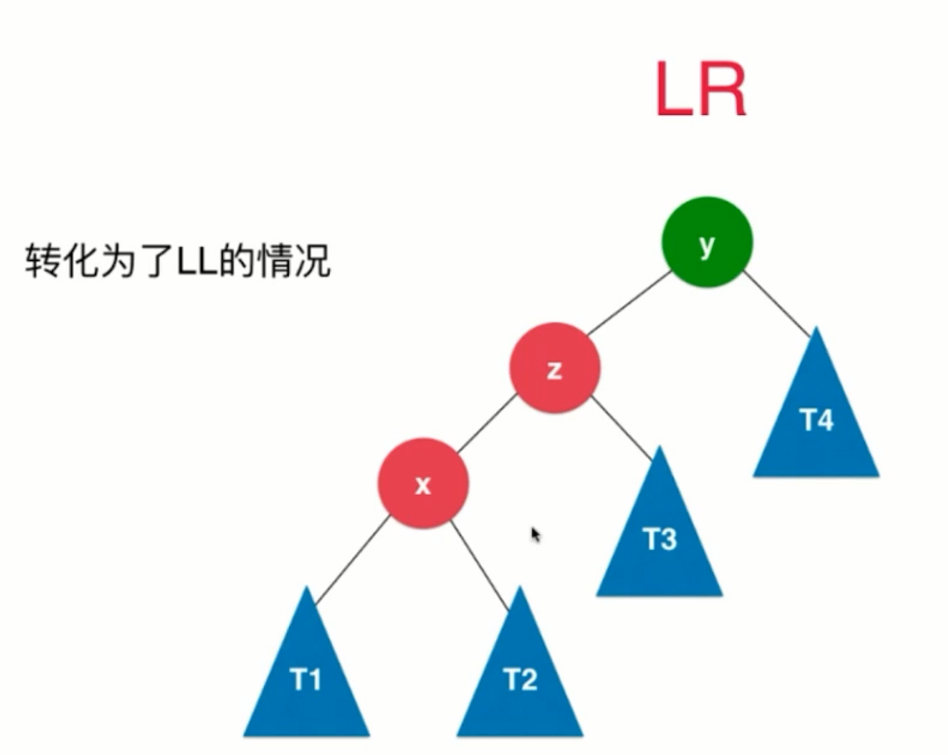
LR：新插入的节点 在 最小不平衡子树的根节点 的左侧的右侧，需要进行左旋左子树，再右旋。

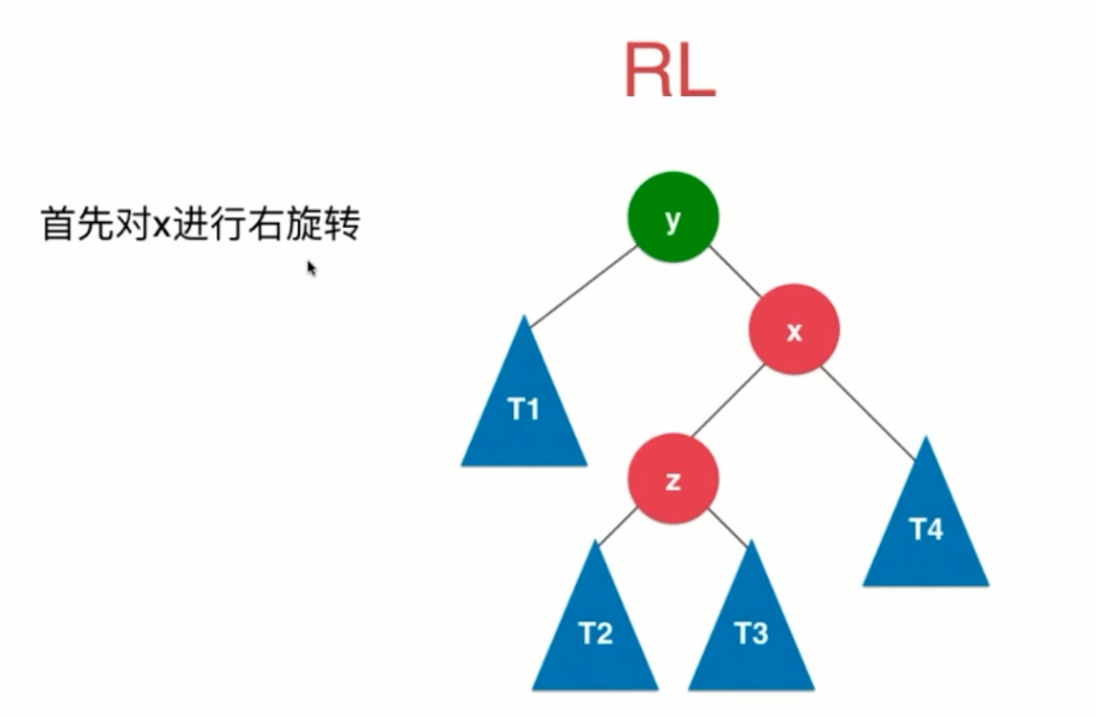
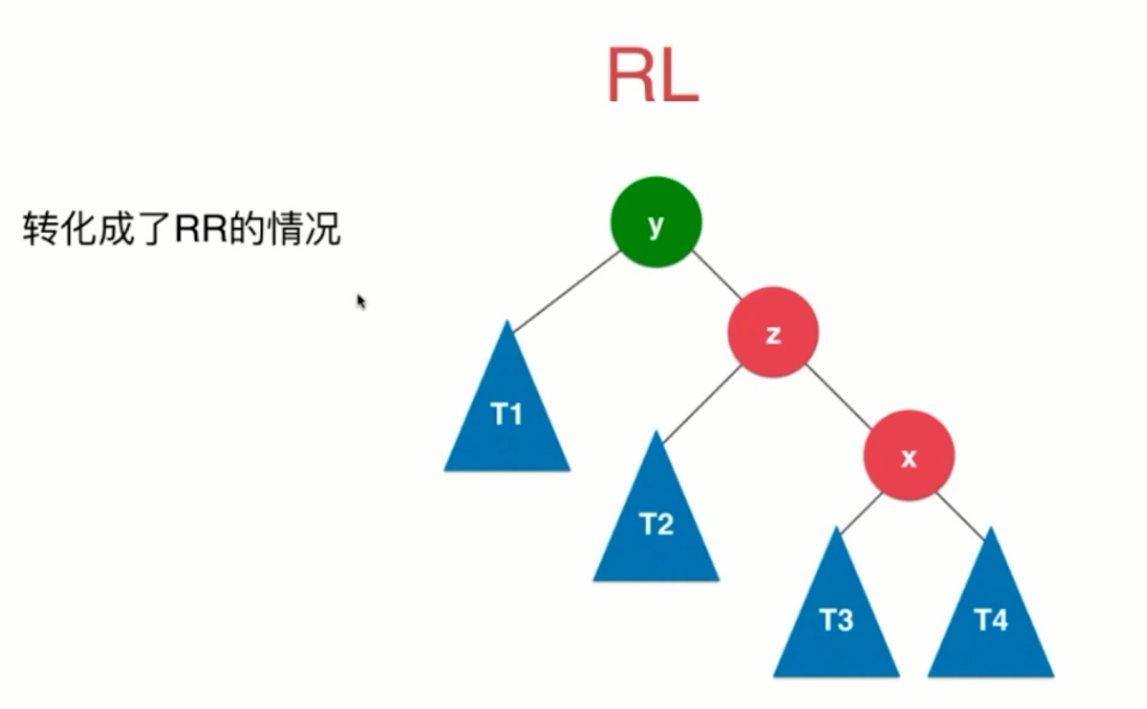
RL：新插入的节点 在 最小不平衡子树的根节点 的右侧的左侧，需要进行右旋右子树，再左旋。

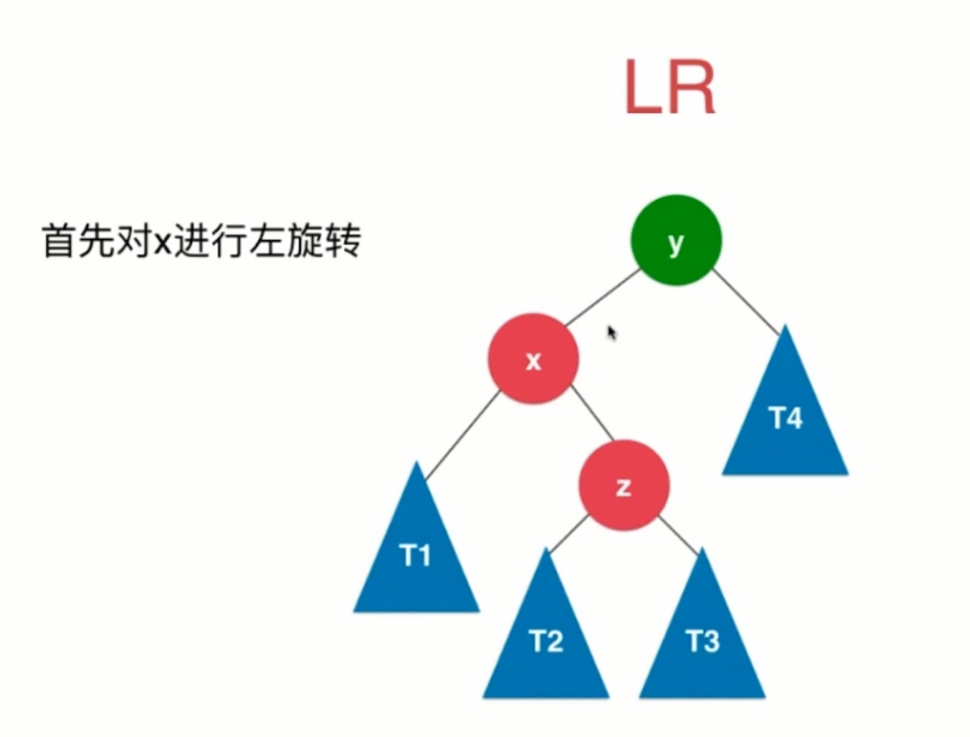
插入节点

插入节点时，需要进行三个新增的步骤

• 高度的更新
• 计算平衡因子
• 平衡的维护，即左右旋转

private Node add(Node node, K key, V value){

    if(node == null){
        size ++;
        return new Node(key, value);
    }

    if(key.compareTo(node.key) < 0)
        node.left = add(node.left, key, value);
    else if(key.compareTo(node.key) > 0)
        node.right = add(node.right, key, value);
    else // key.compareTo(node.key) == 0
        node.value = value;

    // 更新height
    node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));

    // 计算平衡因子
    int balanceFactor = getBalanceFactor(node);

    // 平衡维护
    // LL -> 右旋转
    if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
        return rightRotate(node);

    // RR -> 左旋转
    if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
        return leftRotate(node);

    // LR -> 先左旋根节点的左子树，再右旋转
    if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
        node.left = leftRotate(node.left);
        return rightRotate(node);
    }

    // RL -> 先右旋根节点的右子树，再左旋转
    if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
        node.right = rightRotate(node.right);
        return leftRotate(node);
    }

    return node;
}

删除节点

可以将二分搜索树实现的代码中的删除节点操作，拿过来更改一下。

• 原来代码中删除节点没有维护平衡，所以我们创建一个 retNode，在最后面统一进行维护

• 删除节点进行平衡维护的代码本质 和 插入节点平衡维护代码是一样的，可以复用

• 调用 removeMin(node.right) 方法时，并没有维持节点平衡，可能会将其打破，可以改为remove(node.right,successor.key)；因为代码含义就是删除节点右子树最小节点

• 当key.compareTo(node.key)==0时，后续进行的代码逻辑需要改一下，if,else if,else

• 进行平衡维护时，需要对retNode进行判空操作，否则会出现异常

private Node remove(Node node, K key){

    if( node == null )
        return null;

    Node retNode;
    if( key.compareTo(node.key) < 0 ){
        node.left = remove(node.left , key);
        // return node;
        retNode = node;
    }
    else if(key.compareTo(node.key) > 0 ){
        node.right = remove(node.right, key);
        // return node;
        retNode = node;
    }
    else{   // key.compareTo(node.key) == 0

        // 待删除节点左子树为空的情况
        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            // return rightNode;
            retNode = rightNode;
        }

        // 待删除节点右子树为空的情况
        else if(node.right == null){
            Node leftNode = node.left;
            node.left = null;
            size --;
            // return leftNode;
            retNode = leftNode;
        }

        // 待删除节点左右子树均不为空的情况
        else{
            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            //successor.right = removeMin(node.right);
            successor.right = remove(node.right, successor.key);
            successor.left = node.left;

            node.left = node.right = null;

            // return successor;
            retNode = successor;
        }
    }

    if(retNode == null)
        return null;

    // 更新height
    retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));

    // 计算平衡因子
    int balanceFactor = getBalanceFactor(retNode);

    // 平衡维护
    // LL
    if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
        return rightRotate(retNode);

    // RR
    if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0)
        return leftRotate(retNode);

    // LR
    if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
        retNode.left = leftRotate(retNode.left);
        return rightRotate(retNode);
    }

    // RL
    if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
        retNode.right = rightRotate(retNode.right);
        return leftRotate(retNode);
    }

    return retNode;
}

基于AVL实现集合映射

点击下载-AVLMap.java

点击下载-AVLSet.java

我们底层使用的是基于键值对的 AVL ，所以既可以很方便的实现映射，也可以方便的实现集合。

当实现集合时，不需要value值，我们只需要将其作为Object类型，传null值 即可。