Java-线段树

发表于 | 分类于 | 阅读次数:

为什么需要线段树

1
2
3
4
题目一：
10000个正整数，编号1到10000，用A[1],A[2],A[10000]表示。
修改：无
统计：1.编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 10000.

方法一：对于统计L,R ，需要求下标从L到R的所有数的和，从L到R的所有下标记做[L..R],问题就是对A[L..R]进行求和。这样求和，对于每个询问，需要将(R-L+1)个数相加

方法二：更快的方法是求前缀和,令 S[0]=0, S[k]=A[1..k] ，那么，A[L..R]的和就等于S[R]-S[L-1]，
这样，对于每个询问，就只需要做一次减法，大大提高效率

1
2
3
4
题目二：
10000个正整数，编号从1到10000，用A[1],A[2],A[10000]表示。
修改：1.将第L个数增加C （1 <= L <= 10000）
统计：1.编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 10000.
  • 再使用方法二的话，假如A[L]+=C之后，S[L],S[L+1],,S[R]都需要增加C,全部都要修改，见下表
方法一 方法二
A[L]+=C 修改一个元素 修改R-L+1个元素
求和A[L…R] 计算R-L+1个元素的和 计算两个元素的差

从上表可以看出，方法一修改快，求和慢。 方法二求和快，修改慢。

那有没有一种结构，修改和求和都比较快呢？答案当然是线段树。

线段树

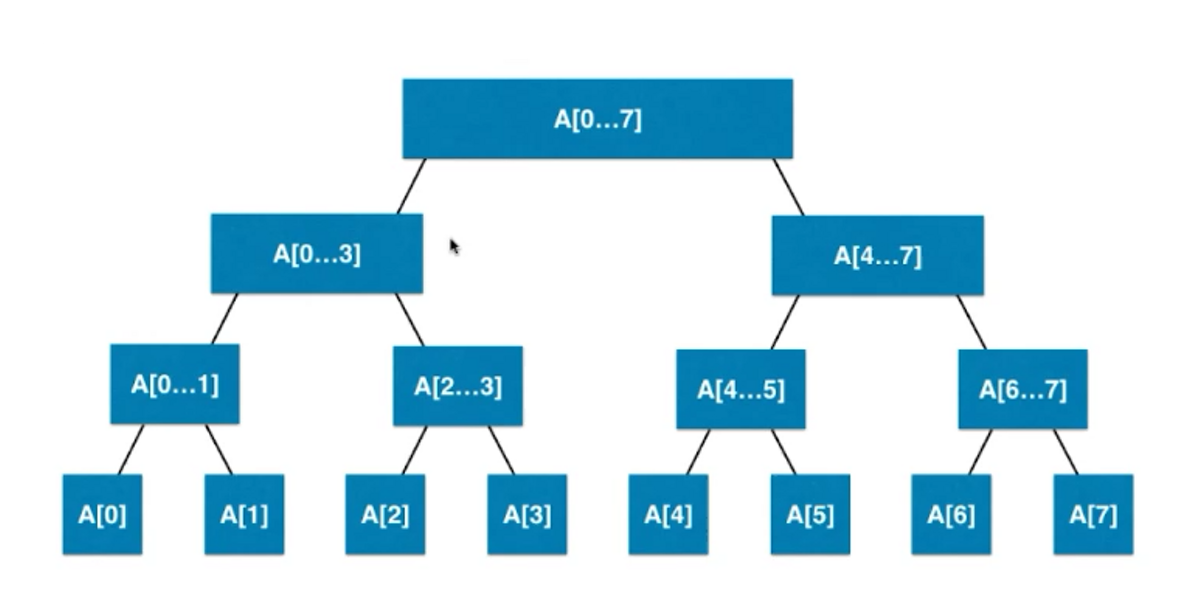
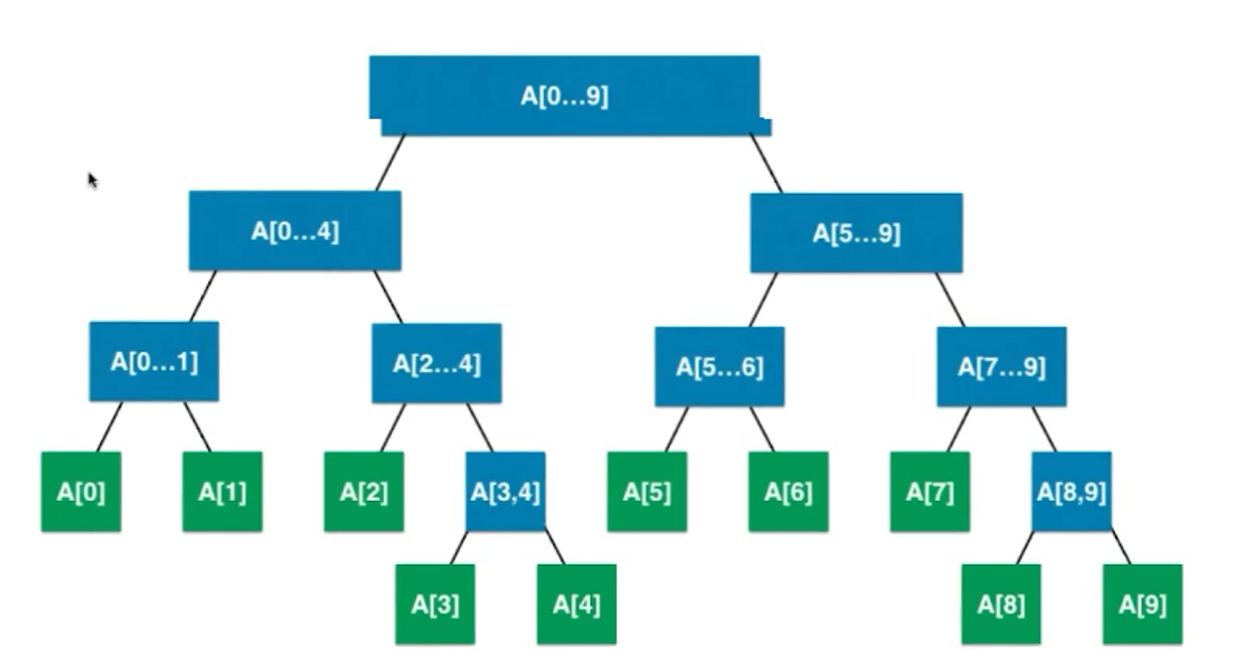
  • 如上我们可以看出线段树不是完全二叉树，而是平衡二叉树，堆也是平衡二叉树

  • 可以将第二张图上的，线段树看作满二叉树，即视缺少的部分为null值

数组表示线段树

线段树是一种二叉树，当然可以像一般的树那样写成结构体，指针什么的。
但是它的优点是，它也可以用数组来实现树形结构，可以大大简化代码。
数组形式适合在编程竞赛中使用，在已经知道线段树的最大规模的情况下，直接开足够空间的数组，然后在上面建立线段树

简单的记法：

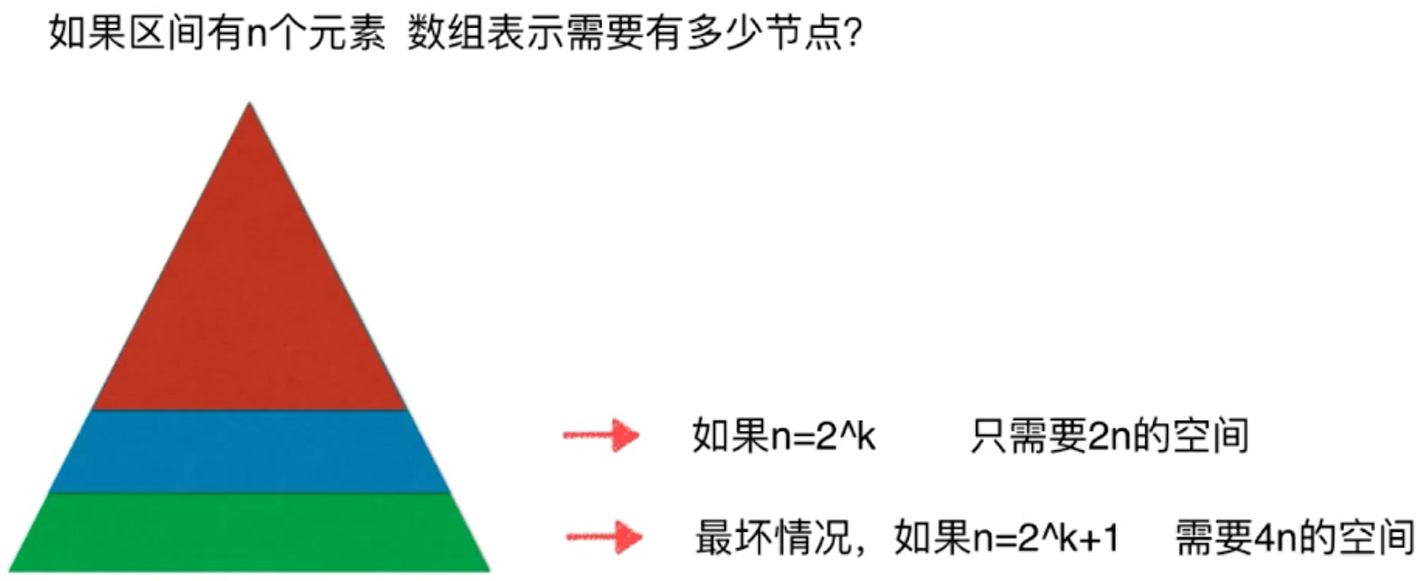
足够的空间 = 数组大小n 的四倍。
实际上足够的空间 = （n向上扩充到最近的2的某个次方）的两倍

举例子：

  • 假设数组长度为5，就需要5先扩充成8，8 * 2=16. 线段树需要16个元素
  • 如果数组元素为8，那么也需要16个元素
  • 所以线段树需要的空间是n的两倍到四倍之间的某个数，一般就开4 * n的空间就好
  • 如果空间不够，可以自己算好最大值来省点空间。

如何表示

  • 假设某个节点的编号为v，那么它的左子节点编号为2 * v，右子节点编号为2 * v+1
  • 然后规定根节点为1，这样一颗二叉树就构造完成了
  • 通常2 * v在代码中写成 v<<1 。 2 * v + 1写成 v<<1|1 （位运算符）

区间加法

用线段树统计的东西或解决的问题，都必须符合区间加法

符合区间加法的例子
数字之和 总数字之和 = 左区间数字之和 + 右区间数字之和
最大公因数（GCD) 总GCD = GCD( 左区间GCD , 右区间GCD )
最大值 总最大值 = Max(左区间最大值，右区间最大值)
不符合区间加法的例子
众数 只知道左右区间的众数，没法求总区间的众数
序列的最长连续零 只知道左右区间的最长连续零，没法知道总的最长连续零

代码实现

融合器

  • 使用融合器有更好的扩展性，完成符合区间加法的操作
1
2
3
public interface Merger<E> {
    E merge(E a, E b);
}
  • 在线段树构造函数中，将该融合器作为参数，在具体实现的时候可以使用匿名内部类
  • 当然也可以使用 Java 8 新特性，Lambda 表达式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class SegmentTree<E> {

    private E[] tree;
    private E[] data;
    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger){

        this.merger = merger;

        data = (E[])new Object[arr.length];
        for(int i = 0 ; i < arr.length ; i ++)
            data[i] = arr[i];

        tree = (E[])new Object[4 * arr.length];
        buildSegmentTree(0, 0, arr.length - 1);
    }
    
}

创建区间

需要注意的是，创建区间方法中，取左右区间中值的时候，可能会 整型大小溢出，要像下面那么写

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// 在treeIndex的位置创建表示区间[l...r]的线段树
private void buildSegmentTree(int treeIndex, int l, int r){

    if(l == r){
        tree[treeIndex] = data[l];
        return;
    }

    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);

    // int mid = (l + r) / 2;
    int mid = l + (r - l) / 2;
    buildSegmentTree(leftTreeIndex, l, mid);
    buildSegmentTree(rightTreeIndex, mid + 1, r);

    tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}

public int getSize(){
    return data.length;
}

public E get(int index){
    if(index < 0 || index >= data.length)
        throw new IllegalArgumentException("Index is illegal.");
    return data[index];
}

// 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index){
    return 2*index + 1;
}

// 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index){
    return 2*index + 2;
}

获取区间值

在线段树中进行对[ queryL，queryR ] 的搜索

  • 首先是对根的左右子树进行判断，判断想获取的区间在左子树，右子树，还是各有一部分
  • 然后进行递归操作，确定准确的区间，并将其返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 返回区间[queryL, queryR]的值
public E query(int queryL, int queryR){

    if(queryL < 0 || queryL >= data.length ||
       queryR < 0 || queryR >= data.length || queryL > queryR)
        throw new IllegalArgumentException("Index is illegal.");

    return query(0, 0, data.length - 1, queryL, queryR);
}

// 在以treeIndex为根的线段树中[l...r]的范围里，搜索区间[queryL...queryR]的值
private E query(int treeIndex, int l, int r, int queryL, int queryR){

    if(l == queryL && r == queryR)
        return tree[treeIndex];

    int mid = l + (r - l) / 2;
    // treeIndex的节点分为[l...mid]和[mid+1...r]两部分

    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    if(queryL >= mid + 1)
        return query(rightTreeIndex, mid + 1, r, queryL, queryR);
    else if(queryR <= mid)
        return query(leftTreeIndex, l, mid, queryL, queryR);

    E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
    E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
    return merger.merge(leftResult, rightResult);
}

更新

更新操作是牵一发而动全身的，不光要进行该单个值的修改，还要对其的祖辈节点进行更改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 将index位置的值，更新为e
public void set(int index, E e){

    if(index < 0 || index >= data.length)
        throw new IllegalArgumentException("Index is illegal");

    data[index] = e;
    set(0, 0, data.length - 1, index, e);
}

// 在以treeIndex为根的线段树中更新index的值为e
private void set(int treeIndex, int l, int r, int index, E e){

    if(l == r){
        tree[treeIndex] = e;
        return;
    }

    int mid = l + (r - l) / 2;
    // treeIndex的节点分为[l...mid]和[mid+1...r]两部分

    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    if(index >= mid + 1)
        set(rightTreeIndex, mid + 1, r, index, e);
    else // index <= mid
        set(leftTreeIndex, l, mid, index, e);

    tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}

实战练习

LeetCode 303

LeetCode 307