Java-集合与映射

发表于 | 分类于 | 阅读次数:

集合（Set）

  • 不能添加重复元素
  • 应用：
    • 客户统计，词汇量统计

实现

1
2
3
4
5
6
7
public interface Set<E> {
    void add(E e);
    boolean contains(E e);
    void remove(E e);
    int getSize();
    boolean isEmpty();
}

基于二分搜索树.

  • 创建一个 Set 接口，定义 Set 的基础方法
  • 创建 BSTSet 类，实现 Set 接口，内部实现二分搜索树的结构
  • 注意：使用泛型后，需继承 Comparable （二分搜索树里的数据必须是可比较的）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
package dataStructure.set;

import dataStructure.BST;

public class BSTSet<E extends Comparable<E>> implements Set<E>{

    private BST<E> bst;

    public BSTSet(){
        bst = new BST<>();
    }

    @Override
    public void add(E e) {
        bst.add(e);
    }

    @Override
    public void remove(E e) {
        bst.remove(e);
    }

    @Override
    public boolean contains(E e) {
        return bst.contains(e);
    }

    @Override
    public int getSize() {
        return bst.size();
    }

    @Override
    public boolean isEmpty() {
        return bst.isEmpty();
    }
}
  • 写完这个后，发现和二分搜索树不是完全一样吗，对！二分搜索树就已经实现了 Set 的所有功能

基于链表

  • 实现Set接口，内部实现LinkedList的结构（前文中自制的）前文地址
  • 除了添加方法需要进行设置一下，其他的都调用链表方法就行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class LinkedListSet<E> implements Set<E> {

    private LinkedList<E> list;

    public LinkedListSet(){
        list = new LinkedList<>();
    }

    public int getSize(){
        return list.getSize();
    }

    public boolean isEmpty(){
        return list.isEmpty();
    }

    public void add(E e){
        if(!list.contains(e))
            list.addFirst(e);
    }

    public boolean contains(E e){
        return list.contains(e);
    }

    public void remove(E e){
        list.removeElement(e);
    }

}

时间复杂度分析

  • 最理想的情况下，是满二叉树，h层的话，一共有2^(h-1)个节点
  • h = log2 (n+1)
  • O(log2 n) = O(log n)

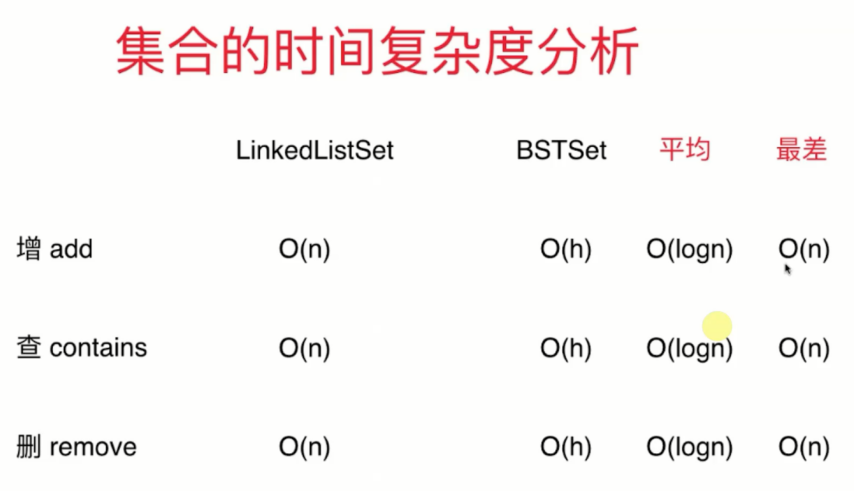
  • 这两种时间复杂度的差距其实是非常大的，可以用一张图来更好的看出来

有序无序

  • 一般来说，集合中元素可以轻易的进行排序，就是有序集合
  • 有序集合基于搜索树实现的
  • 无序集合有 基于链表实现的、基于哈希表实现的

映射（Map）

  • 存储（键，值）数据对应的数据结构（Key，Value）就是映射
  • 根据Key ，寻找Value
  • 非常容易通过链表或二分搜索树实现

实现

1
2
3
4
5
6
7
8
9
10
public interface Map<K, V> {

    void add(K key, V value);
    V remove(K key);
    boolean contains(K key);
    V get(K key);
    void set(K key, V newValue);
    int getSize();
    boolean isEmpty();
}

基于链表

  • 需要创建一个 getNode 的方法来辅助实现 增删改查 方法 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
public class LinkedListMap<K, V> implements Map<K, V> {

    private class Node{
        public K key;
        public V value;
        public Node next;

        public Node(K key, V value, Node next){
            this.key = key;
            this.value = value;
            this.next = next;
        }

        public Node(K key, V value){
            this(key, value, null);
        }

        public Node(){
            this(null, null, null);
        }

        @Override
        public String toString(){
            return key.toString() + " : " + value.toString();
        }
    }

    private Node dummyHead;
    private int size;

    public LinkedListMap(){
        dummyHead = new Node();
        size = 0;
    }

    @Override
    public int getSize(){
        return size;
    }

    @Override
    public boolean isEmpty(){
        return size == 0;
    }

    private Node getNode(K key){
        Node cur = dummyHead.next;
        while(cur != null){
            if(cur.key.equals(key))
                return cur;
            cur = cur.next;
        }
        return null;
    }

    public boolean contains(K key){
        return getNode(key) != null;
    }

    public V get(K key){
        Node node = getNode(key);
        return node == null ? null : node.value;
    }

    public void add(K key, V value){
        Node node = getNode(key);
        if(node == null){
            dummyHead.next = new Node(key, value, dummyHead.next);
            size ++;
        }
        else
            node.value = value;
    }

    public void set(K key, V newValue){
        Node node = getNode(key);
        if(node == null)
            throw new IllegalArgumentException(key + " doesn't exist!");

        node.value = newValue;
    }

    public V remove(K key){

        Node prev = dummyHead;
        while(prev.next != null){
            if(prev.next.key.equals(key))
                break;
            prev = prev.next;
        }

        if(prev.next != null){
            Node delNode = prev.next;
            prev.next = delNode.next;
            delNode.next = null;
            size --;
            return delNode.value;
        }

        return null;
    }

}

基于二分搜索树

二分搜索树

定义二分搜索树类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class BSTMap<K extends Comparable<K>, V> implements Map<K, V> {

    private class Node{
        public K key;
        public V value;
        public Node left, right;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
        }
    }
    private Node root;
    private int size;

    public BSTMap(){
        root = null;
        size = 0;
    }
    
}
辅助方法
1
2
3
4
5
6
7
8
9
10
11
12
13
// 返回以node为根节点的二分搜索树中，key所在的节点
private Node getNode(Node node, K key){

    if(node == null)
        return null;

    if(key.equals(node.key))
        return node;
    else if(key.compareTo(node.key) < 0)
        return getNode(node.left, key);
    else // if(key.compareTo(node.key) > 0)
        return getNode(node.right, key);
}
常见方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int getSize(){
    return size;
}

public boolean isEmpty(){
    return size == 0;
}

public boolean contains(K key){
    return getNode(root, key) != null;
}

public V get(K key){
    Node node = getNode(root, key);
    return node == null ? null : node.value;
}
增加元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 向二分搜索树中添加新的元素(key, value)

public void add(K key, V value){
    root = add(root, key, value);
}

// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){

    if(node == null){
        size ++;
        return new Node(key, value);
    }

    if(key.compareTo(node.key) < 0)
        node.left = add(node.left, key, value);
    else if(key.compareTo(node.key) > 0)
        node.right = add(node.right, key, value);
    else // key.compareTo(node.key) == 0
        node.value = value;

    return node;
}
删除元素
  • 删除元素和二分搜索树中的删除元素很相似
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
// 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null)
            return node;
        return minimum(node.left);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){

        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }

    // 从二分搜索树中删除键为key的节点
    @Override
    public V remove(K key){

        Node node = getNode(root, key);
        if(node != null){
            root = remove(root, key);
            return node.value;
        }
        return null;
    }

    private Node remove(Node node, K key){

        if( node == null )
            return null;

        if( key.compareTo(node.key) < 0 ){
            node.left = remove(node.left , key);
            return node;
        }
        else if(key.compareTo(node.key) > 0 ){
            node.right = remove(node.right, key);
            return node;
        }
        else{   // key.compareTo(node.key) == 0

            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }

            // 待删除节点右子树为空的情况
            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }

            // 待删除节点左右子树均不为空的情况

            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;

            node.left = node.right = null;

            return successor;
        }
    }

复杂度

有序无序

  • 根据键是否有顺序性，判断映射为有序无序
  • 基于搜索树实现的是有序的映射
  • 基于哈希表实现的是无序的映射

集合和映射关系

  • 可以互相转换
  • 如：有了映射的底层实现，可以将value看为0，这样就实现了集合

相关问题